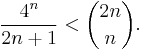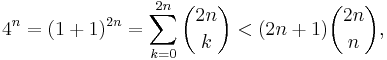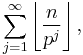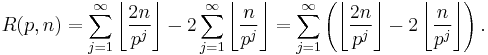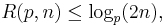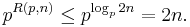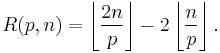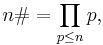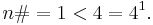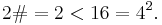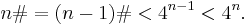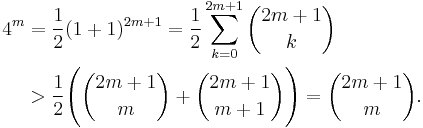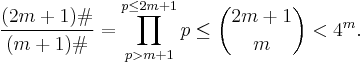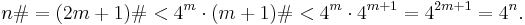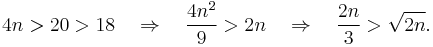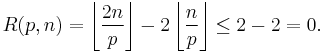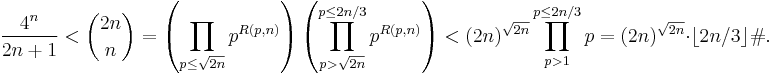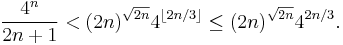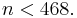Proof of Bertrand's postulate

In mathematics, Bertrand's postulate (actually a theorem) states that for each n ≥ 2 there is a prime p such that n < p < 2n. It was first proven by Pafnuty Chebyshev, and a short but advanced proof was given by Srinivasa Ramanujan. The gist of the following elementary but involved proof by contradiction is due to Paul Erdős; the basic idea of the proof is to show that a certain binomial coefficient needs to have a prime factor within the desired interval in order to be large enough.

1 Lemmas and computation
2 Proof of Bertrand's Postulate
3 References

The argument in the proof establishes a contradiction by comparing two facts:

The binomial coefficient 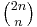$\textstyle\binom{2n}{n}$ is "large" in a precise sense (Lemma 1), and
If Bertrand's postulate fails for n, then all of the prime factors of this binomial coefficient are "small" (a combination of Lemma 3 and the negation of Bertrand's postulate).

It is then shown by some extended computation (relying mostly on Lemma 2 and Lemma 4) that the second fact is inconsistent with the first one. Therefore Bertrand's postulate must hold. In order to present the main argument of the proof intelligibly, these lemmas and a few auxiliary claims are proved separately first.

Lemmas and computation

Lemma 1: A lower bound on the central binomial coefficients

Lemma: For any integer n > 0, we have

$\frac{4^n}{2n%2B1} < \binom{2n}{n}.\$

Proof: Applying the binomial theorem,

$4^n = (1 %2B 1)^{2n} = \sum_{k = 0}^{2n} \binom{2n}{k} < (2n %2B 1) \binom{2n}{n},\$

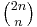since $\textstyle\binom{2n}{n}$ is the largest term in the sum, and the sum has 2n+1 terms.

Lemma 2: An upper bound on prime powers dividing central binomial coefficients

For a fixed prime p, define R(p,n) to be the highest natural number x, such that p^x divides 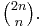$\textstyle\binom{2n}{n}.$

Lemma: For any p, we have p^R(p,n) ≤ 2n.

Proof: The exponent of p in n! is (see Factorial#Number theory):

$\sum_{j = 1}^\infty \left\lfloor \frac{n}{p^j} \right\rfloor,\$

so we get

$R(p,n) =\sum_{j = 1}^\infty \left\lfloor \frac{2n}{p^j} \right\rfloor - 2\sum_{j = 1}^\infty \left\lfloor \frac{n}{p^j} \right\rfloor =\sum_{j = 1}^\infty \left(\left\lfloor \frac{2n}{p^j} \right\rfloor - 2\left\lfloor \frac{n}{p^j} \right\rfloor\right).$

But each term of the last summation can either be 0 (if n / p^j mod 1 < 1/2) or 1 (if n / p^j mod 1 ≥ 1/2) and all terms with j > log_p(2n) are 0. Therefore

$R(p,n) \leq \log_p(2n),\$

and we get:

$p^{R(p,n)} \leq p^{\log_p{2n}} = 2n.\$

This completes the proof of the lemma.

Lemma 3: The exact power of a large prime in a central binomial coefficient

Lemma: For 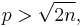$p > \sqrt{2n},$ we have

$R(p,n) = \left\lfloor \frac{2n}{p} \right\rfloor - 2\left\lfloor \frac{n}{p} \right\rfloor.\$

Proof: Using the same sum for R(p,n) as in Lemma 2, we see that since p² > 2n, in fact only the first term is nonzero; this term is exactly the right-hand side of the above equation.

Lemma 4: An upper bound on the primorial

We estimate the primorial function,

$n\# = \prod_{p \leq n} p,\$

where the product is taken over all prime numbers p less than or equal to n.

Lemma: For all n ≥ 1, we have n# < 4ⁿ.

Proof: The proof is by mathematical induction. First the base cases:

n = 1: n# is the empty product:

$n\# = 1 < 4 = 4^1.\$

n = 2: 2 is prime:

$2\# = 2 < 16 = 4^2.\$

n > 2 and n is even: Since every even number greater than 2 is composite, we have by the induction hypothesis:

$n\# = (n-1)\# < 4^{n-1} < 4^n.\$

n > 2 is odd. Let n = 2m + 1 with m > 0; then since all the terms in the following binomial expansion are positive we have:

$\begin{align} 4^m &= \frac{1}{2}(1 %2B 1)^{2m %2B 1} = \frac{1}{2}\sum_{k = 0}^{2m%2B1} \binom{2m %2B 1}{k} \\ &> \frac{1}{2} \Biggl(\binom{2m %2B 1}{m} %2B \binom{2m %2B 1}{m %2B 1}\Biggr) = \binom{2m %2B 1}{m}. \end{align}$

Each prime p with m + 1 < p ≤ 2m + 1 divides 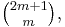$\textstyle\binom{2m %2B 1}{m},$ giving us:

$\frac{(2m %2B 1)\#}{(m %2B 1)\#} = \prod_{p > m %2B 1}^{p \leq 2m %2B 1} p \leq \binom{2m%2B1}{m} < 4^m.\$

By induction, (m + 1)# < 4^{m + 1}, so:

$n\# = (2m %2B 1)\# < 4^m \cdot (m %2B 1)\# < 4^m \cdot 4^{m %2B 1} = 4^{2m %2B 1} = 4^n.\$

Thus the lemma is proven.

Computation

We collect here a numerical claim which comes up in the proof.

If 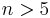$n>5$ , then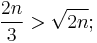 $\frac{2n}{3} > \sqrt{2n};$

To prove 1, observe that

$4n>20>18 \quad\Rightarrow\quad \frac{4n^2}{9} > 2n \quad\Rightarrow\quad \frac{2n}{3} > \sqrt{2n}.$

Proof of Bertrand's Postulate

Assume there is a counterexample: an integer n ≥ 2 such that there is no prime p with n < p < 2n.

If 2 ≤ n < 468, then p can be chosen from among the prime numbers 3, 5, 7, 13, 23, 43, 83, 163, 317, 631 (each being less than twice its predecessor) such that n < p < 2n. Therefore n ≥ 468.

There are no prime factors p of 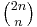$\textstyle\binom{2n}{n}$ such that:

2n < p, because every factor must divide (2n)!;
p = 2n, because 2n is not prime;
n < p < 2n, because we assumed there is no such prime number;
2n / 3 < p ≤ n: by computation 1 we have 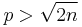$p > \sqrt{2n}$ , so Lemma 3 applies, and by rearranging the inequalities 2n/3 < p and n ≥ p we deduce that n/p ≥ 1 and 2n/p < 3. Combining these results, we get

$R(p,n) = \left\lfloor \frac{2n}{p} \right\rfloor - 2\left\lfloor \frac{n}{p} \right\rfloor \leq 2 - 2 = 0.\$

Therefore, every prime factor p satisfies p ≤ 2n/3.

When 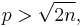$p > \sqrt{2n},$ the number 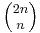$\textstyle {2n \choose n}$ has at most one factor of p. By Lemma 2, for any prime p we have p^R(p,n) ≤ 2n, so the product of the p^R(p,n) over the primes less than or equal to 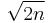$\sqrt{2n}$ is at most 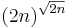$(2n)^{\sqrt{2n}}$ . Then, starting with Lemma 1 and decomposing the right-hand side into its prime factorization, these bounds give:

$\frac{4^n}{2n %2B 1} < \binom{2n}{n} = \left(\prod_{p \le \sqrt{2n}} p^{R(p,n)}\right) \left(\prod_{p > \sqrt{2n}}^{p \le 2n/3} p^{R(p,n)}\right) < (2n)^{\sqrt{2n}} \prod_{p > 1}^{p \leq 2n/3} p = (2n)^{\sqrt{2n}} \cdot \lfloor 2n/3 \rfloor\#.\$

Using Lemma 4, this simplifies:

$\frac{4^n}{2n %2B 1} < (2n)^{\sqrt{2n}} 4^{\lfloor 2n/3 \rfloor} \leq (2n)^{\sqrt{2n}} 4^{2n/3}.\$

This gives us the contradiction:

$n < 468.\$

Thus no counterexample to the postulate is possible.

References

Aigner, Martin, G., Günter M. Ziegler, Karl H. Hofmann, Proofs from THE BOOK, Fourth edition, Springer, 2009. ISBN 978-3-642-00855-9.